No Straight Lines Make Up My Life

← August 8, 2011 →

⊕
One example ($N=6$).

Take a unit circle, and inscribe a regular $N$-gon.

Pick one vertex. Draw lines from that vertex to all the other vertices (two of these lines are edges of the $N$-gon, the rest are interior to the $N$-gon).

What is the product of the lengths of these lines?

⊕
$N=3$, with additional lines that help us deduce the side length.

We can start with simple examples. For $N=3$ we need to know the lengths of the sides of an equilateral triangle whose center is 1 unit from the vertices. By drawing the angle bisectors / medians / altitudes (which are all the same for an equilateral triangle) we can decompose the triangle in 30˚-60˚-90˚ right triangles with hypotenuse 1. The side of interest of one of those smaller triangles has length $\frac{\sqrt{3}}{2}$, so the equilateral triangle has side $\sqrt{3}$ and the product we’re after is $\sqrt{3}\times\sqrt{3}=3$.

Curious. Let’s check $N=4$.

The decomposition in this case is even simpler! We can draw just four 45˚-45˚-90˚ triangles with side length 1 and hypotenuse $\sqrt{2}$. So, the product we’re after is $2\times\sqrt{2}\times\sqrt{2}=4$, where the terms are the inner diagonal and the two sides of the square, respectively.

⊕
$N=2$

In fact, if $N$=2, the polygon is degenerate, but we can consider the points at ±1—so the length of the one line 2!

$N$	product of lengths
2	2
3	3
4	4

Does this pattern hold forever? Does it generalize into higher dimensions?

I immediately checked the tetrahedron and cube inscribed in the unit sphere, and found that there was no obvious pattern in 3 dimensions.

I struggled to find a proof in 2D. I was able to reduce the problem to proving

$\prod_{n=1}^{N-1} \sin\left( \frac{n \pi}{N} \right) = \frac{N}{ 2^{N-1}}$

but got no further.

My friend Will offered the following proof:

Consider a regular $N$-gon in the complex plane with vertices at the $N^{th}$ roots of unity $\omega^n$ where $\omega=e^{2\pi i/N}$. Let 1 be the distinguished vertex, so the product of the lengths to all the other vertices is

$\prod\text{lengths} = \prod_{n=1}^{N-1} |1-\omega^n| = \left|\prod_{n=1}^{N-1} (1-\omega^n) \right|$

Now consider the polynomial identityThis is in some sense the definition of the roots of unity.

$z^N-1 = \prod_{n=0}^{N-1} \left(z-\omega^n\right)$

which is just the factorization of the left hand side into linear factors. Differentiating both sides with respect to $z$ and setting $z=1$,

$N = \sum_{k=0}^{N-1}\prod_{n=0,n\neq k}^{N-1}\left(1-\omega^n\right).$

But now note that if $k\neq 0$ then the product on the right hand side includes a factor of $1-\omega^0=0$ and so vanishes. Thus only $k=0$ contribues,

$N = \prod_{n=1}^{N-1}\left(1-\omega^n\right).$

Combining this with the first equation yields

$\prod\text{lengths} = N.$

QED.

The reliance on complex numbers immediately explains why there was no pattern in three dimensions. I would be interested to learn if there is any similar identity that takes advantage of the quaternions or octonions.

I designed a graphic inspired by this identity, and gave Will a printed copy as thanks for this enlightening proof.

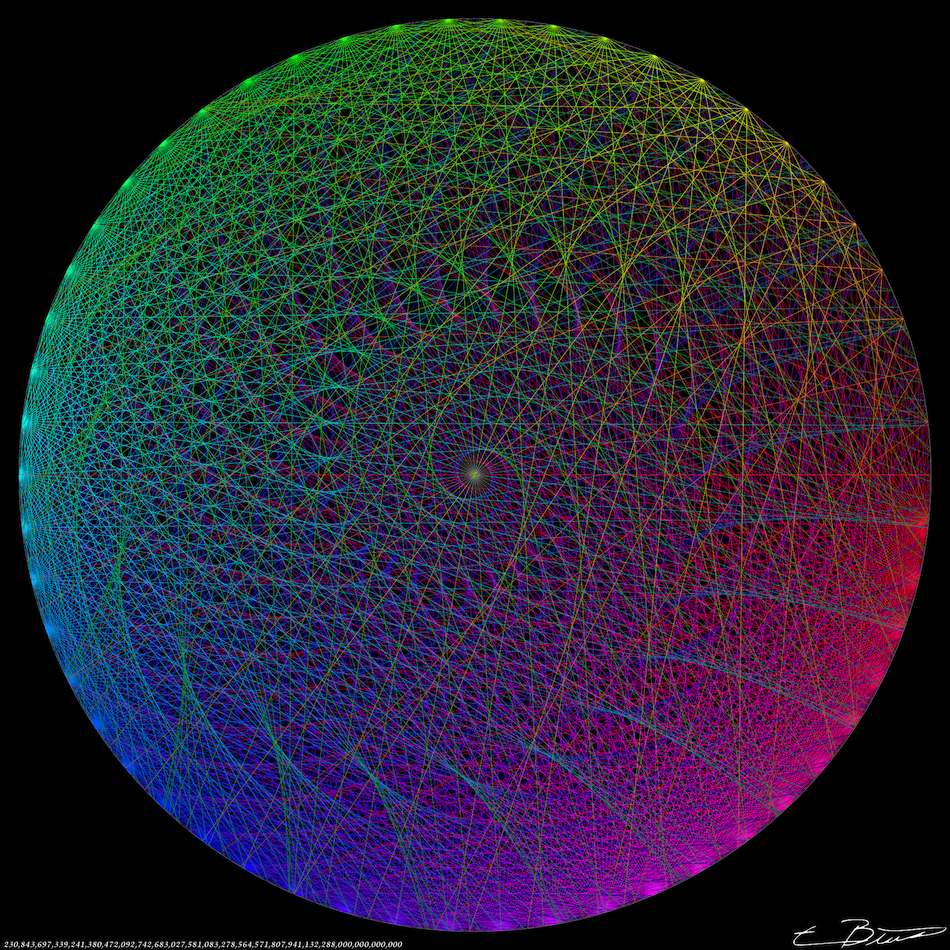
If we take the bounding circle to have radius 1, the product of length of all the lines in this figure is exactly

230 843 697 339 241 380 472 092 742 683 027 581 083 278 564 571 807 941 132 288 000 000 000 000

or $54!$, as it is all the figures for $N=2$ to $N=54$, each a different color, superimposed.

Subsequently, I came across a purely algebraic proof that does not require differentiation.

← August 8, 2011 →

Natural Wonder

Evan Berkowitz

© Evan Berkowitz

No Straight Lines Make Up My Life