Tyger Tyger, burning bright

← October 3, 2011 →

⊕Rev. Mod. Phys. 23, 21 (1951)
hep-th/9405029
Ohanian Ch. 6+8

⊕I first prepared these notes for a 90-minute lecture for the first semester of Graduate Quantum Mechanics in 2011.

The Factorization, Operator,

or Supersymmetric Method

In quantum mechanics we are, quite generally, intersted in studying Hamiltonians (in rescaled variables) like

In one dimension we usually mean ​$x\in (-\infty,\infty)$, while in three dimensions we usually mean ​$x = r \in [0,\infty)$ and ​$V=V_\ell$ where ​$\ell$ is a partial wave label, so that we just worry about the radial pieceReducing to just a radial coordinate only works for spherically symmetric potentials. .

Let us focus on a special class of Hamiltonians: those derivable from a superpotential ​$W(x)$. Let’s defineRecall \(i \frac{d}{dx}\) is Hermitian, so \(\frac{d}{dx}^\dagger = -\frac{d}{dx}\)

From these operators we can build two Hamiltonians,

and its partner

where the sign of the second term is the only difference between the two.

Immediately we can prove a nice theorem:

Theorem: The eigenenergies of these Hamiltonians are nonnegative.

Proof: For any state ​$\left|\phi\right\rangle$ the matrix element of ​$H_1$ is

and similar reasoning establishes the claim for ​$H_2$.∎

The two Hamiltonians differ only by the sign of the derivative term for the superpotential—does this establish a deep connection?

Theorem: They have almost the same spectrum!

Proof: Suppose ​$\left|\phi_n\right\rangle$ are the energy eigenstates of ​$H_1$:

Applying ​$A$ to the above,

but we know ​$H_2 = AA^\dagger$ so the second equality can be written

so if we let ​$\left|\psi_n\right\rangle = A \left|\phi_n\right\rangle$ then ​$\left|\psi_n\right\rangle$ is an eigenstate of ​$H_2$ with energy ​$E_1^{(n)}$!

This of course works the other way—hit

with ​$A^\dagger$ and you will find

That’s it. The two Hamiltonians have precisely the same spectrum. Any loopholes?

Just one.

If ​$A \left|\phi_n\right\rangle = 0$ or ​$A^\dagger \left|\psi_n\right\rangle = 0$—i.e. if one of the Hamiltonians has a zero-energy eigenstate, then we cannot successfully do the regrouping because the state is destroyed.

Can we find these destroyed states?

Yes! ​$A \left|\phi_n\right\rangle = 0$ and ​$A^\dagger \left|\psi_n\right\rangle = 0$ are linear, first-order ODEs:

We can use the method of the integrating factor. It is simple to check thatThe lower bounds on the integrals simply readjust the proportionality constant.

solve those differential equations, respectively.

Now we can check the normalizability of these states. For ​$\phi_0(x)$,

so we need ​$\int^x dy\; W(y)$ to go to ​$\infty$ as ​$x\rightarrow\infty$, so that ​$W(x)$ must fall slowly or grow at large ​$x$.

On the other hand, for ​$\psi_0(x)$, we find

so we need ​$\int^x dy\; W(y)$ to go to ​$-\infty$ as ​$x\rightarrow\infty$.

These two behaviors are clearly incompatible, so we conclude that ​$H_1$ and ​$H_2$ have the same spectrum except at most one has a zero energy eigenstate.∎

In one dimension, for any Hamiltonian ​$H$, if you can find its ground state and adjust the constant part correctly, you can get ​$W(x) = -\frac{d}{dx}\ln \phi_0(x)$ so that ​$H=H_1$ and you can build ​$H_2$. But ​$H_2$ is not generically simple, so this is not a good way of solving most problems.

In three dimensions, it isn’t always possible to perform this feat, but it is in a large number of cases. In fact, Schrödinger solved the hydrogen atom this way in the 1940s.Proc. Roy. Irish Acad. A 48, 9-16 (1940/1941).

The Harmonic Oscillator ​$W(x) = x$

⊕
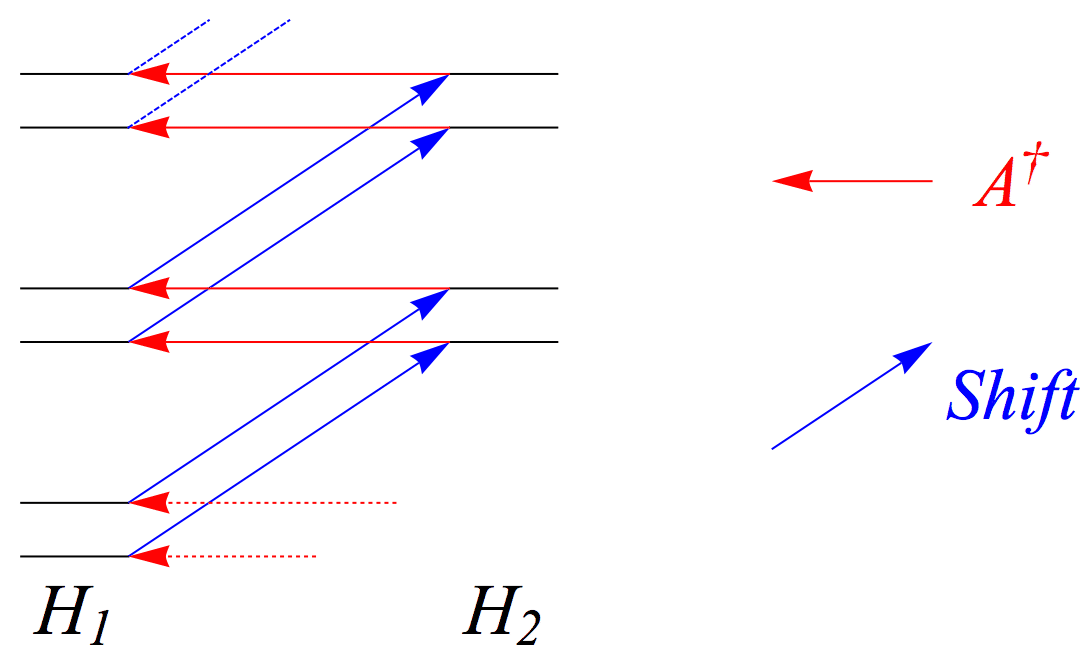
Using the shift and ladder operator to find new higher-energy states in the spectrum of \(H_1\).

​$H_1$ and ​$H_2$ have the same spectrum, but are only different by a constant. How could that be?

For every energy eigenvalue there must be another one a constant amount higher, because we can do the constant shift from ​$H_1$ to ​$H_2$ and then use ​$A^\dagger$ to find a state in the spectrum of ​$H_1$.

⊕

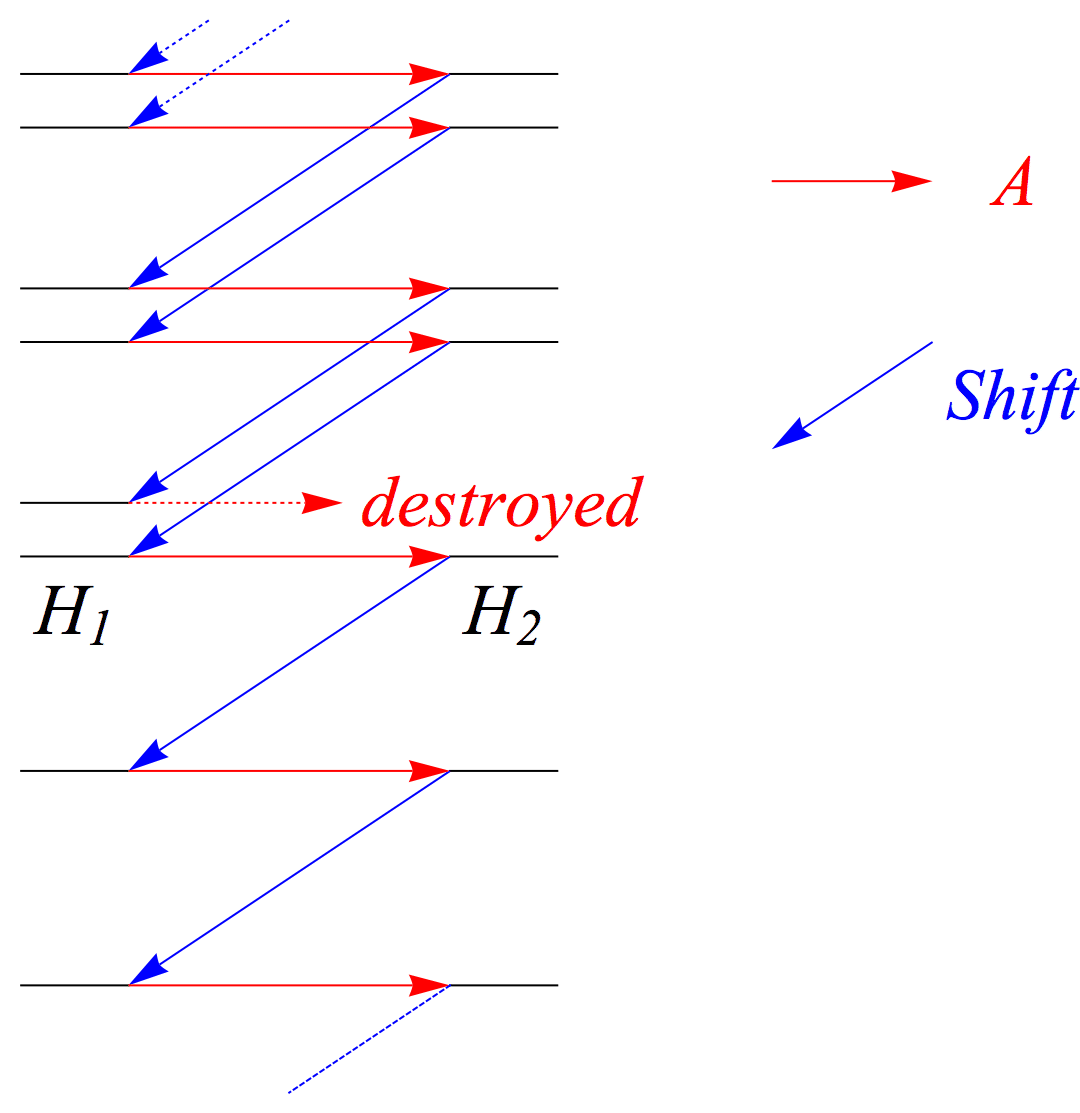
Going to higher energies forever in this fashion is perfectly fine. Going down is doable too, but can create issues.

Since the equation ​$\frac{d\phi_0}{dx}+W(x)\phi_0(x) = 0$ is a first order, linear ODE, it has only one solutionUp to an overall normalization. . So, if there are multiple towers of evenly-spaced states, only one of them can have a state that gets destroyed. The spectra of the two Hamiltonians still match exactly but for this destroyed state. But, since no other state can get destroyed, one can forever find states with less energy (again, by a constant amount), and this must eventually violate the non-negativity theorem we proved above.

So, these extra states cannot be in the spectrum, by reductio ad absurdum. Moreover, you cannot find multiple perfectly-aligned towers of states because of the uniqueness theorem for ​$\frac{d\phi_0}{dx}+W(x)\phi_0(x) = 0$. The harmonic oscillator has but one semi-infinite tower of evenly spaced states.

Have we done anything new? No, not for this example. If you check you will find ​$A^\dagger = \sqrt{2}a^\dagger$ and ​$A = \sqrt{2}a$ where \(a\) and \(a^\dagger\) are the usual ladder operators for the harmonic oscillator.

The Coulomb Potential ​$W^{(\ell)}(r) = -\frac{\ell+1}{r} + \frac{1}{2(\ell+1)}$

⊕Again, first presented by Schrödinger, Proc. Roy. Irish Acad. A 48, 9-16 (1940/1941).

The way the three-dimensional central potential problems tend to work is that you can, by a clever choice of superpotentials, construct relationships between ​$H_2^{(\ell)}$ and ​$H_1^{(\ell+1)}$.

For the Coulomb superpotential

one finds

so there is a constant shift between different \(\ell\) and supersymmetric partners.

This method also works for the three-dimensional isotropic harmonic oscillator,

but I will not go through the algebra or logic here.

Infinite Square Well

Suppose you restrict, in one dimension, to ​$-\frac{\pi}{2} \leq x \leq \frac{\pi}{2}$ and let

Then,

a constant potential with hard boundaries—the infinite square well—and

This potential looks like it ought to be extremeley difficult to solve, except that we know its spectrum matches the infinite square well. That is,

You can figure this out more precisely.

What’s In A Name?

⊕Caveat Lector: this section is not very precise. I welcome pedagogical clarifications or simplifications.

Supersymmetry, or SUSY, is a symmetry that theorists like for its beauty and its ability to resolve some of the theoretical problems in quantum field theory:

• Gauge coupling unification
• Provides dark matter candidates
• Solves the hierarchy problem / provides naturalness.

It guarantees that particle species come in pairsOr larger multiplets, depending on the amount of supersymmetry of equal mass called superpartners.

It is unclear if SUSY is a symmetry of nature: we know of no superpartners, even though we expected them to be produced at the Large Hadron Collider.

If you restrict to particles at rest, a state with one boson species and one fermion specied can be specified by

where ​$n_b$ is a nonnegative integer representing how many bosons there are, and ​$n_\uparrow, n_\downarrow$ are either 0 or 1by Pauli exclusion and describe how many fermions there are.

A state is bosonic if ​$n_\uparrow + n_\downarrow \equiv 0$ (mod 2) and fermionic otherwise.

We can partition all the states into bosonic and fermionic sectors and define the Hamiltonian of this system to be

which can be constructed out of

with ​$A$ a fermionic operator. One can check that ​$\{Q,Q^\dagger\}=H$, if we recognize ​$H_b=H_1$ and ​$H_f=H_2$.

​$Q$ and ​$Q^\dagger$ are supersymmetry generators in the superalgebra that take us between the bosonic and fermionic sectors.

The full superalgebra is

The first lines imply that the fermion number is conserved.

← October 3, 2011 →